النمذجة و موازنة الانحياز والتباين
التحفيز
من وقت إلى آخر اجد نفسي أتصفح كتاب Elements of Statistical Learning. الكتاب يحوي على الكثير من الإضاحات والرسومات البيانية لكن لفت انتباهي الرسومات الموجودة حول موضوع موازنة الإنحياز والتباين. هذا الموضوع مهم جدا والكثير يخفى عليه عواقب إهماله. لذلك قررت أن ادون حول الموضوع وأبعث الحياة لتلك الرسومات البيانية.
نبذة عن نظرية التعلم الإحصائي
نظرية التعلم الإحصائي هي أحد ابعاد المنهج العلمي الذي أسسه إبن الهيثم. النظرية توفر نطاق عمل لتطوير نماذج تنبؤية يمكن تقديرها من خلال البيانات المجمعة. بشكل مبسط, النظرية تنص على وجود دالة حقيقية تفسر علاقة متغير معين بمتغير آخر أو عدة متغيرات. هذه الدالة دائما ما تكون مجهولة. لذلك يقوم الباحثين بجمع البيانات لتقدير تلك الدالة. هذه الدوال الحقيقة ليست سهلة في التقدير لأنها تضم عوامل أو حدود لامتناهية. لحسن الحظ, كثير من تلك الحدود بإمكاننا تجاهلها لضئل تأثيرها على المخرجات النهائية. في الحقيقة علماء الإحصاء يصفون تلك الحدود بالضجيج وتمثل بحد واحد يسمى الحد العشوائي. يمكننا تمثيل ما ذكرناه رياضيا كالتالي
صعوبات التقدير
طرق تقدير الدالة الحقيقة كثيرة و متعددة لن نفصل فيها هنا لكن كلها تتشارك في خطة سير العمل.
- جمع البيانات
- قسمة البيانات إلى مجموعتين. (مجموعة تدريب و مجموعة اختبار)
- تحديد عدد و نوع المدخلات للنموذج
- صنع نموذج تقديري للدالة الحقيقة بإستخدام مجموعة التدريب وتقليص الخطأ
- تقييم النموذج بإستخدام مجموعة الاختبار
بالنظر إلى هذه الخطوات, قد يتبادر إليك أن عملية التقدير سهلة. لكن الحقيقة هي ان في كل خطوة هناك موارد كثيرة للخطأ. ففي خطوة جمع البيانات مثلا يشترط على الباحث أن يقوم بجمع بيانات خالية من انحيازات كثيرة حتى تمثل العينة بشكل صحيح ارض الواقع. كذلك الأمر نفسه ينطبق على خطوة قسمة البيانات. لكن الصعوبة الحقيقة والخطأ الذي يقع فيه الكثير من الباحثين هو تحديد عدد ونوع المدخلات للنموذج. لأن زيادة عدد المدخلات يؤدي إلى فرص التخصيص(التباين) وقلتها يؤدي إلى فرط التعميم (الانحياز).
موازنة الانحياز والتباين
جهلنا بعدد حدود الدالة الحقيقية يضعنا في مأزق. فنحن لا نعرف كم حد للدالة وأي منها له تأثير كبير وأي منها مجرد ضجيج. أحد الحيل التي ابتكرها الإحصائيون هو قسمة البيانات إلى مجموعتي تدريب واختبار لتقييم جودة التقدير. الهدف هنا أن نستنتج نموذج يقلل مقدار الخطأ في كلتا المجموعتين. حتى نشهد مدى فاعلية هذه الحيلة سوف أقوم بصنع عدة محاكاة تجسد اداء النموذج في كلتا المجموعتين مع زيادة عدد الحدود تدريجيا.
محاكاة تقدير النموذج
الدالة الحقيقة
لنفترض ان الدالة الحقيقة هي كالتالي
وهذه شكل الدالة
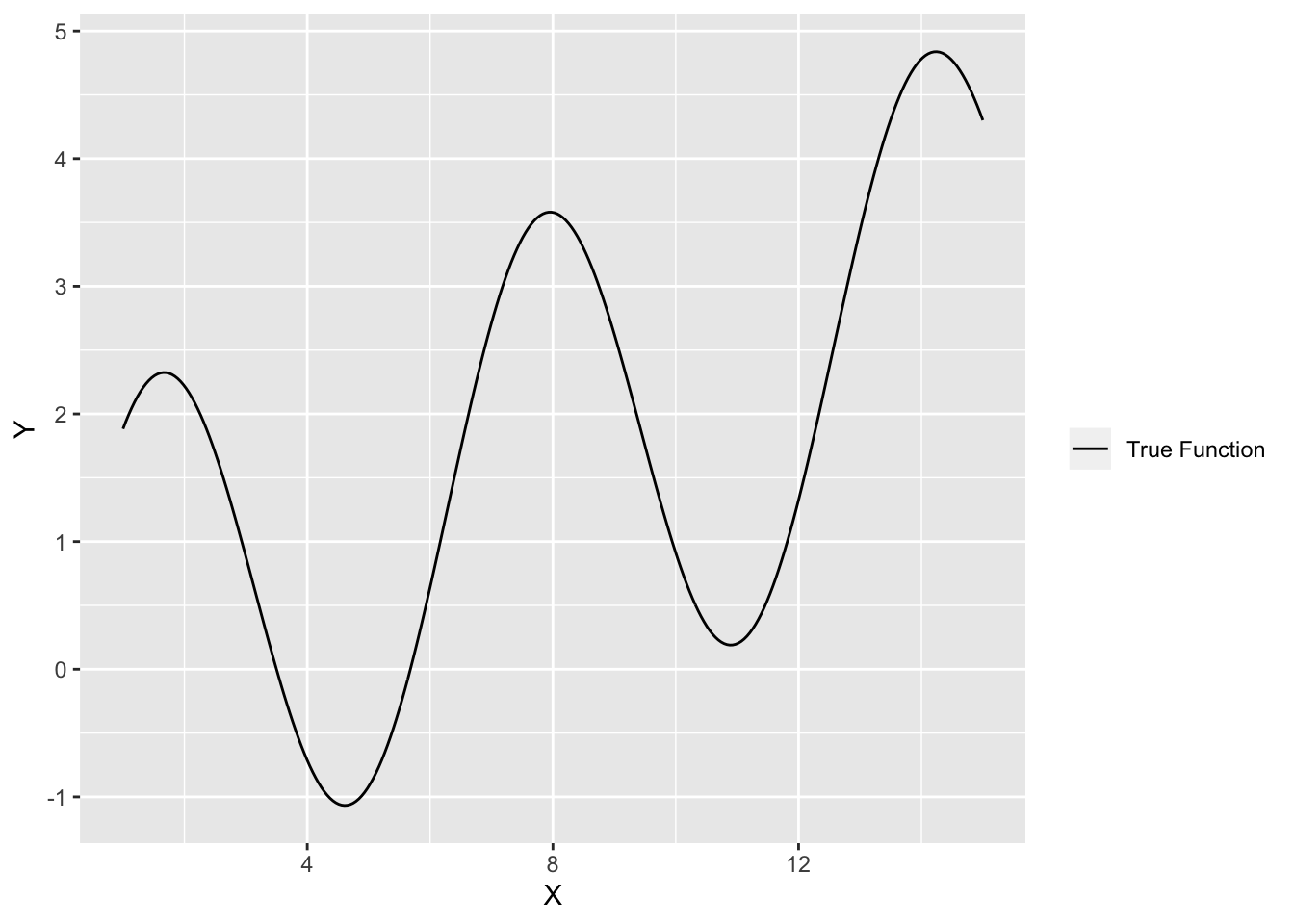
هذه الدالة تفسر ارتباط المتغير بالمتغير . تذكر نحن نجهل هذه الدالة ومهمتنا تقديرها
مجموعة التدريب والإختبار
لنفرض أننا قمنا بجمع البيانات حول و ثم قسمناها إلى مجموعتين وقمنا بتصويرها كالتالي
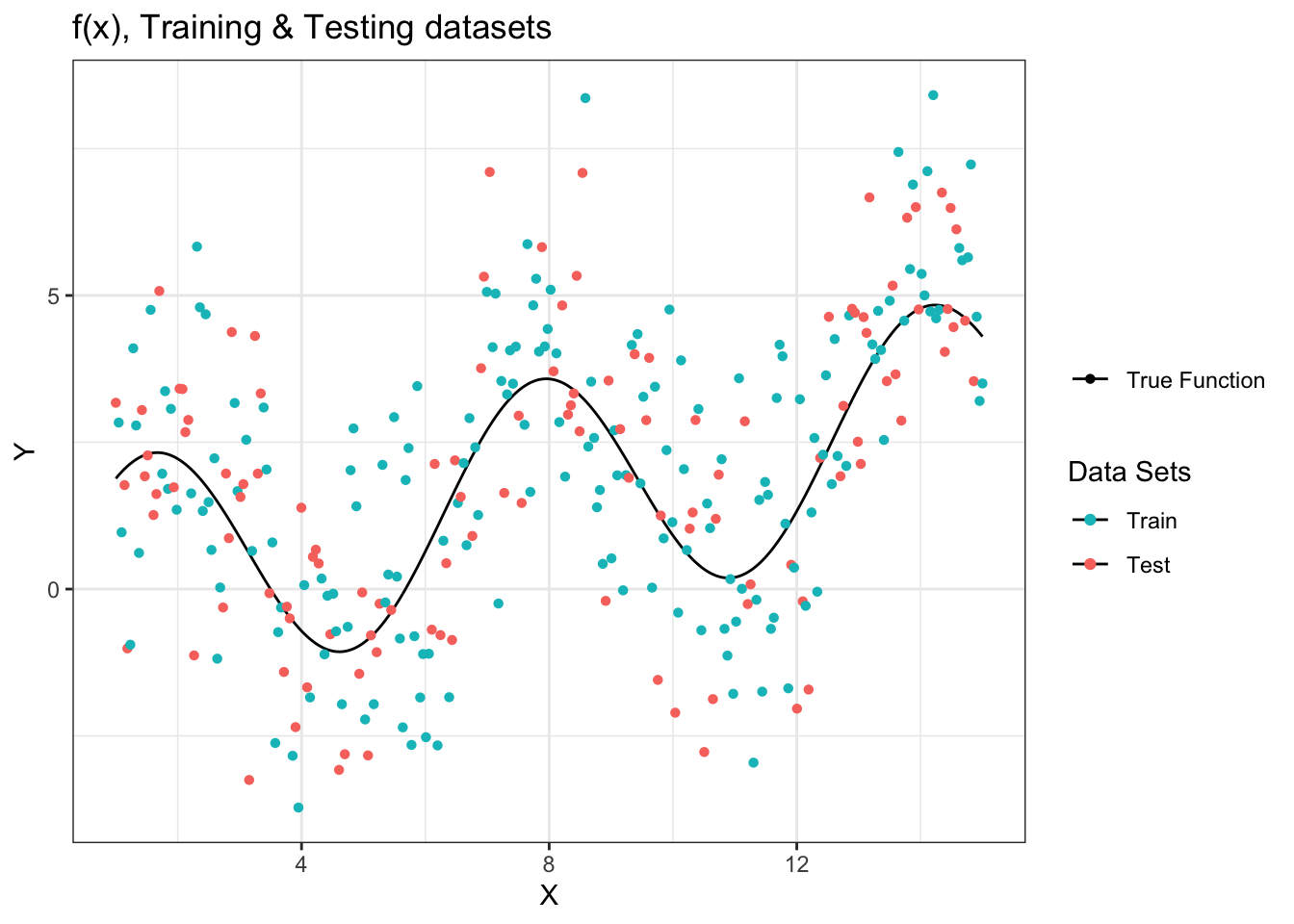 لاحظ أن البيانات لا تنطبق على خط الدالة الحقيقة لأنها تحتوي على ضجيج عشوائي
لاحظ أن البيانات لا تنطبق على خط الدالة الحقيقة لأنها تحتوي على ضجيج عشوائي
تحديد عدد الحدود للنموذج
الآن دعنا نبدأ بتصوير الدالة المقدرة مع زيادة عدد الحدود فيها بحد واحد وسوف نزيد عدد الحدود في كل مرة.
#full code to create "g_animated" is avialable on my github
#https://github.com/Hussain-Alsalman/Arabian_Analyst_Blog/blob/master/content/post/2020-02-15-bias-vs-variance.Rmd
animate(g_animated,fps = 5)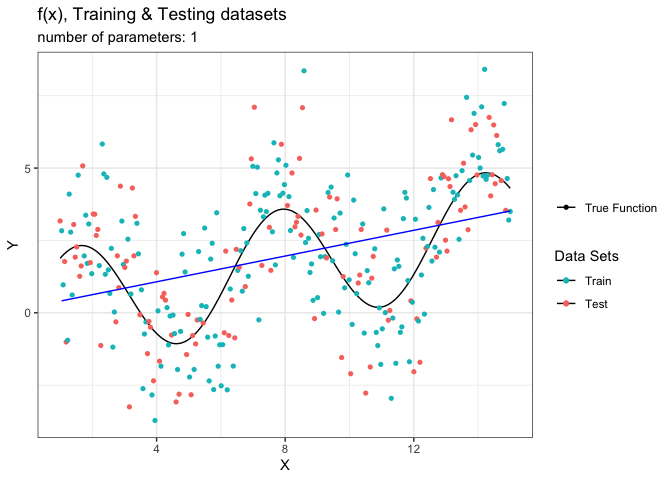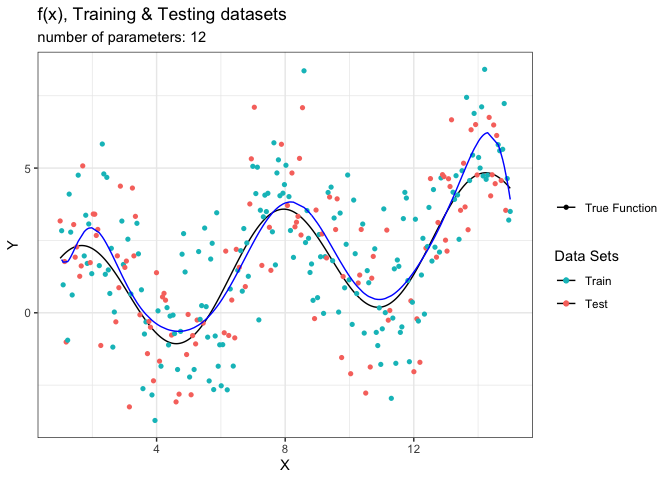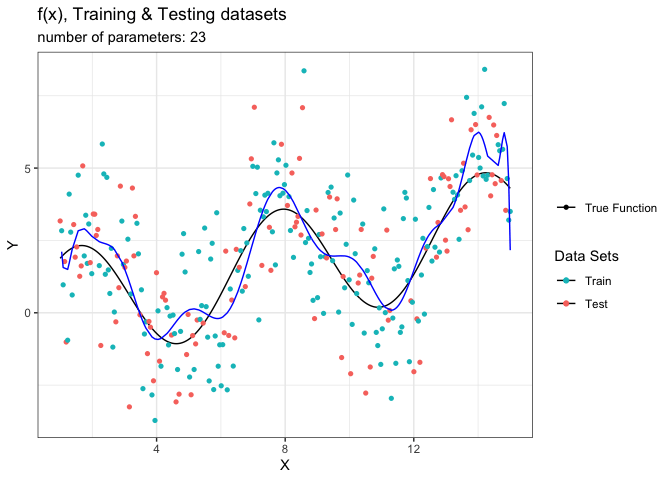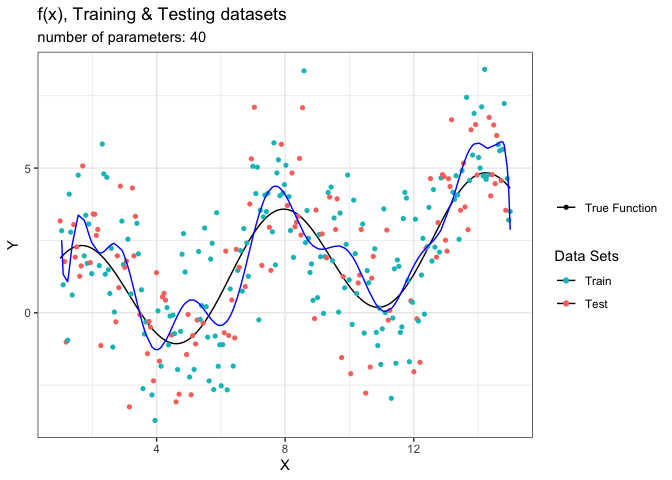
لاحظ تغير شكل الدالة المقدرة باللون الأزرق مع زيادة عدد الحدود. تبدأ المحاكاة بحد واحد فقط وهذا خط مستقيم وهو غير كافي لتقدير الدالة الحقيقة (فرط التعميم). في حين أن النموذج التقديري يظهر تحسن كبير عندما نصل إلى ثمان حدود. لكن مع زيادة العوامل يبدأ النموذج بالتعرج ومحاولة استيعاب الضجيج (فرط التخصيص).
الأداء في مجموعة التدريب والأختبار
دعنا الآن نستطلع أثر زيادة عدد الحدود في النموذج على متوسط الخطأ لكل من المجموعتين (التدريب والاختبار). حتى نتمكن من ذلك, سنقوم بمحاكاة بناء النموذج ألف مرة لكل حد وحساب متوسط الخطأ.
#full code to create "te_tr_g" object is avialable on my github
#https://github.com/Hussain-Alsalman/Arabian_Analyst_Blog/blob/master/content/post/2020-02-15-bias-vs-variance.Rmd
animate(te_tr_g,fps = 8)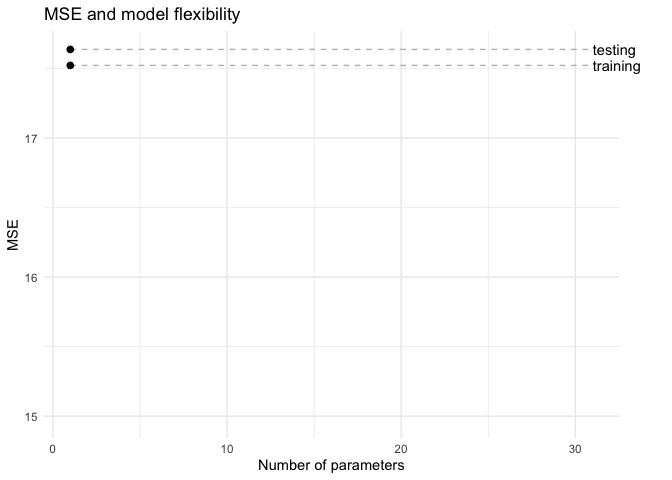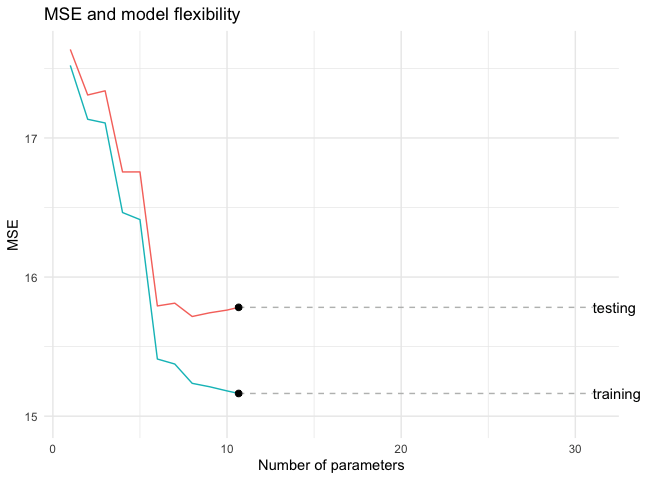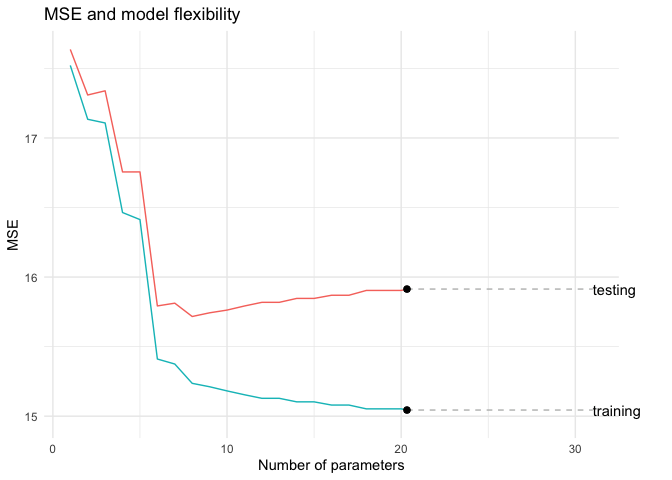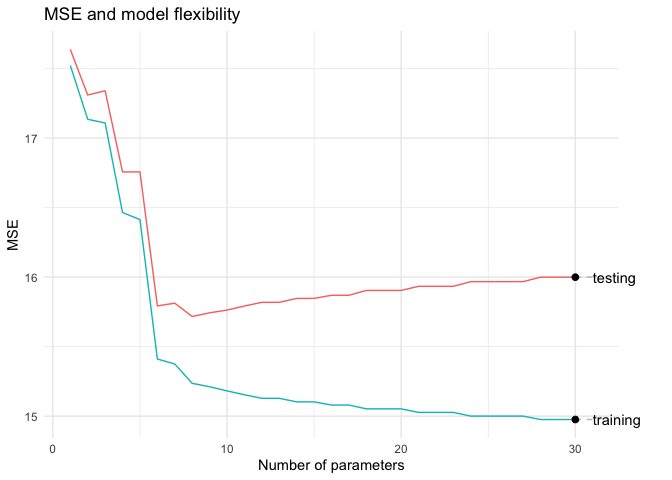
#full code to create "anim" object is avialable on my github
#https://github.com/Hussain-Alsalman/Arabian_Analyst_Blog/blob/master/content/post/2020-02-15-bias-vs-variance.Rmd
animate(anim,fps = 8)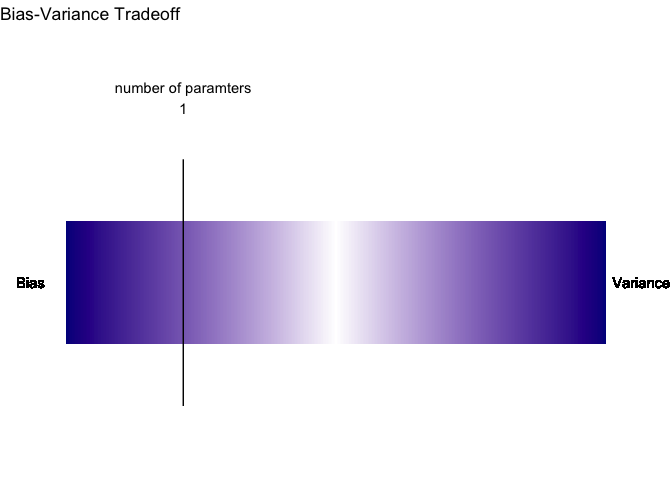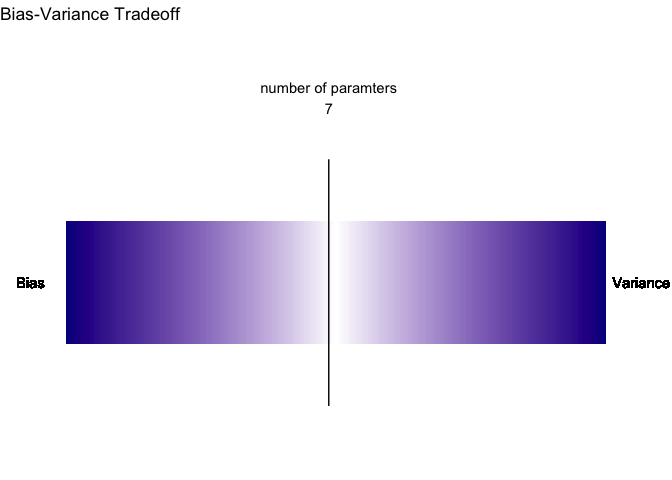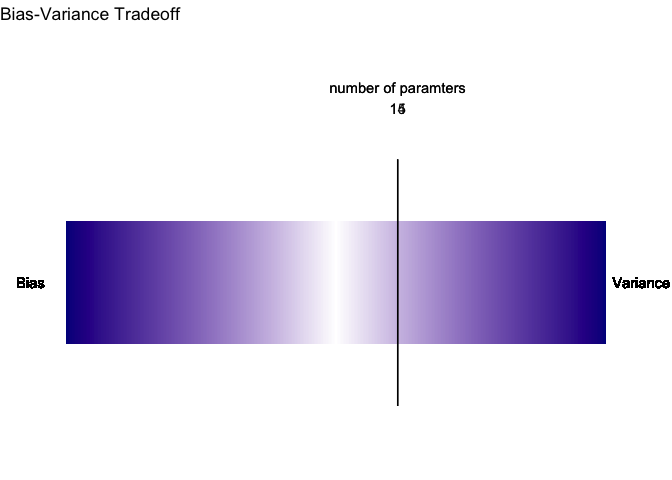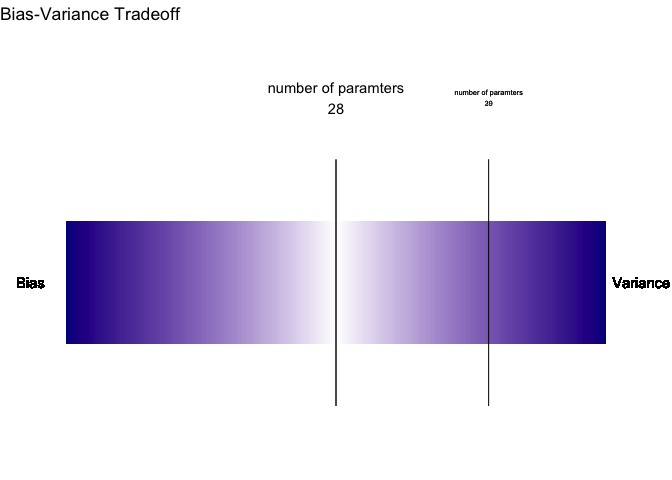
لاحظ أننا بدأنا بمتوسط خطأ كبير لكلتا المجموعتين وذلك بسبب فرط التعميم أي ان النموذج بسيط جدا وليس كافي لتقدير الدالة الحقيقية. لكن مع زيادة عدد الحدود بين ٦ و ٨ تمكنا من تقليص متوسط الخطأ في كلتا المجموعتين.
لاحظ أن متوسط الخطأ يستمر في الهبوط في مجموعة التدريب بينما يبدأ بالإرتفاع في مجموعة الأختبار وذلك بسبب فرط التخصيص أي ان النموذج لا يمكن استخدامه بشكل عام بل هو خاص بمجموعة التدريب.
الخلاصة
موازنة الانحياز والتباين هو شَرَكًا نصبته الطبيعة لتحدي علماء البيانات ولقد وقع فيه الكثير. لذلك يجدر بعالم البيانات أن يتخذ الخطوات الازمة لتفادي الوقوع في فرط التخصيص والتعميم للنماذج التي يقوم بتطويرها. هناك طرق كثيرة لم يسعنا التطرق إليها لتجنب هذا الخطأ منها - التحقق المتقاطع (Cross Validation) - جمع بيانات اكبر - استخدام طريقة الضبط (regularization)
جرب بنفسك
كامل الكود تجده هنا