التسلسلات الزمنية : النموذج المبسط

مقدمة

هذا المقال هو الثاني من سلسلة المقالات التي نتناول فيها موضوع التسلسلات الزمنية. لذلك انصحك أن تقرأ المقال الأول إن كنت لم تقرأه بعد. في هذا المقال سوف نناقش بعض الرموز الرياضية المهمة. آيضا سنقوم بالغوص في التركيبة الأساسية لعناصر نموذج التسلسلات الزمنية وكيفية تقديرها. كذلك سنقوم بمناقشة طريقة التهذيب (smoothing) للتسلسل الزمني و تفكيك اي تسلسل إلى عناصره الأساسية. وسنختم المقال كالعادة بالأمثلة

حتى اﻵن كل ما قمنا بفعله في المقال السابق هو إستعراض الرسم البياني و تحليل ما يبدو لنا من انماط أو تغيرات موسمية. اﻵن حان الوقت لنقاش جوانب متقدمة في الموضوع وبالنسبة لي أكثر متعة وتشويق.

بعض الرموز الرياضية

بما أننا سوف ننظر إلى نماذج التسلسلات الزمنية، يجدر بنا أولا تعلم بعض الرموز الرياضية التي تستخدم لتمثيل تلك النماذج. إن معرفة هذه الرموز سوف تساعدنا ليس فقط على إستعاب مقال اليوم ولكن ايضا ستعيننا على قراءة اي مقال أو بحث علمي عن التسلسلات الزمنية.

في نماذج التسلسلات، دائما نرمز للوقت بحرف t وعدد العينات بحرف n. أيضا كما تعودنا، نرمز للمتغير بحرف x فتمثيل بسيط لبيانات التسلسلات سوف يكون شكله كالتالي

\[x_{t}: t=1,...,n\]

عادة ما تختصر بالشكل التالي

\[x_{t}\]

رمز آخر يجب علينا تعلمه وهو lead time او المهلة ويرمز له بالحرف k. نستخدم هذا الرمز عادة عندما نريد أن نمثل قيمة مستقبلية للمتغير. لذلك عادة ما نرى هذا هذا الرمز مجموع برمز الوقت كما هو في المعادلة التالية.

\[t+k\]

نماذج التسلسلات الزمنية

النموذج المبسط للتسلسلات الزمنية هو كالتالي

\[x_{t}=m_{t}+s_{t}+z_{t}\]

حيث X كما ذكرنا سابقا تمثل البيانات للمتغير. بالنسبة إلى الرمز m فهو ما نقدر به النمط. أما s فهو التغيرات الموسمية وآخيرا z هو عنصر العشوائية في المعادلة. لو تجاهلنا عنصر العشوائية للحظة, ستجد أنه لو عرفنا اثنين من المتغيرات في المعادلة سيمكننا تقدير الثالث. و بما أن المتغير x دائما ما يكون متوفر لدينا ﻷنه يمثل البيانات, فتقدير النمط او التغيرات الموسمية من هذه المعادلة يمكننا من معرفة الأخر

الجدير بالذكر هنا أن هناك نوعين من النماذج، النموذج الجمعي والنموذج الضربي. وكما يدل الأسم، في النموذج الأول تكون العلاقة بين العناصر الثلاث جمعية أما في النموذج الثاني فالعلاقة ضربية أو طردية.

كيفية تقدير تلك العناصر

هناك طرق كثيرة لتقدير عناصر نموذج التسلسل الزمني يصعب علينا نقاشها كلها في هذا المقال. لكن في الوقت الحالي سوف نكتفي بستخدام اسهلها حسابيا لتقدير عنصر الموسمية. الطريقة هي أن نقوم بحساب المتوسط المتحرك حول قيمة معينة في وقت معين. قبل أن نقوم بذلك دعنا نعرف ما هو المتوسط الحسابي المتحرك. المتوسط الحسابي المتحرك هو المتوسط الحسابي لعدد معين من المتغير في التسلسل الزمني حول نقطة معينة في ذلك التسلسل.

تفاصيل طريقة حساب المتوسط الحسابي المتحرك

لنفترض أنه لدينا قيم شهرية للمتغير معين مطلوب مننا تقدير عنصر الموسمية فيها. أولا نقوم بتحديد الفترة الموسمية. الفترة الموسمية هنا ١٢ شهر. تبدأ السنة بشهر يناير وتنتهي بشهر ديسمبر. بما أن عدد الشهور عدد زوجي، ستكون لدينا القيمة في منتصف الفترة 6.5 أو بتعبير رياضي t = 6.5 . هنا نواجه مشكلة لأن طريقة المتوسط الحسابي المتحرك تقتضي أن تكون قيمة t قمية غير كسرية. لحل تلك المشكلة سنقوم بحساب المتوسط الحسابي المتحرك لفترتين ثم نأخذ متوسطهم الحسابي. الفترة الأولى ستكون بين يناير (t=1) وديسمبر(t = 12) والثانية ستكون بين فبراير (t=2) ويناير (t =13). بهذه الطريقة سيكون لدينا المتوسط الحسابي المتحرك للفترة t = 7. هذه الحيلة الرياضية تعرف بالـ centering وبشكل عام تكون المعادلة كالتالي

\[{\hat{m}_{t} = \frac{\frac{1}{2}x_{t-6}+x_{t-5}+ ... + x_{t-1}+x_{t}+x_{t+1}+...+x_{t+5}+\frac{1}{2}x_{t+6}}{12}}\]

بعد الحصول على تقدير للنمط، يمكننا إشتقاق قيمة اللتغيرات الموسمية بكل سهولة من خلال هذه المعادلة

\[\hat{s}_{t} = x_{t} - \hat{m}_{t}\]

تهذيب التسلسلات الزمنية

هناك طريقتين لتهذيب التسلسلات الزمنية والتخلص من التغيرات الموسمية. في الحقيقة الطريقة الأولى ناقشناها للتو وهي طريقة المتوسط الحسابي المتحرك. فمجموعة القيم التي تم حساب المتوسط الحسابي المتحرك لها هي مجموعة تم تهذيبها لتمثيل النمط العام للمتغير.

أما الطريقة الثانية فهي خوارزمية تعرف بـ Loess وهي إختصار لـ locally weighted scatter-plot smoothing. هذه الطريقة تمتاز بأنها لا تتأثر بوجود القيم الشاذة في بيانات التسلسل الزمني. تفاصيل هذه الطريقة تعتبر معقدة بالنسبه لهدف هذا المقال لكن بإختصار شديد, طريقة Loess تعتمد على بناء نماذج انحدارات خطية على مجموعات محلية من البيانات بقصد تهذيبها

مثال عملي

سوف نقوم بتفكيك التسلسل الزمني لمستوى استهلاك الطاقة الكهربائية في استراليا بين عام 1958 إلى 1990 بإستخدام خوارزمية LOESS. لحسن الحظ في لغة R هناك دالة بسيط تقوم بهذه العملية المعقدة. هذه الدالة هي ()decompose . حتى نبدأ دعنا نقوم بتحميل البيانات وتحويلها إلى تسلسل زمني في بيئة R.

library("here")
www <-  here("static", "data", "cbe.dat")
CBE <-  read.table(www,header =  TRUE)
Elec.ts <- ts(CBE[, 3], start =  1958, freq =  12)

ملاحظة: يوجد بيانات اخرى في هذا الملف كمستوى استهلاك الشكولاته والبيرة لنفس المدة الزمنية, لذلك قمنا بإختيار العمود الثالث والذي يتحو على بيانات مستوى استهلاك الطاقة.

الأن كل ما علينا هو أن نضع التسلسل الزمني في تلك الدالة العجيبة ونقوم بتمثيل كل عنصر بالرسم البياني لتتضح لنا الصورة.

Elec.decom <- decompose(Elec.ts, type =  "mult")
plot(Elec.decom)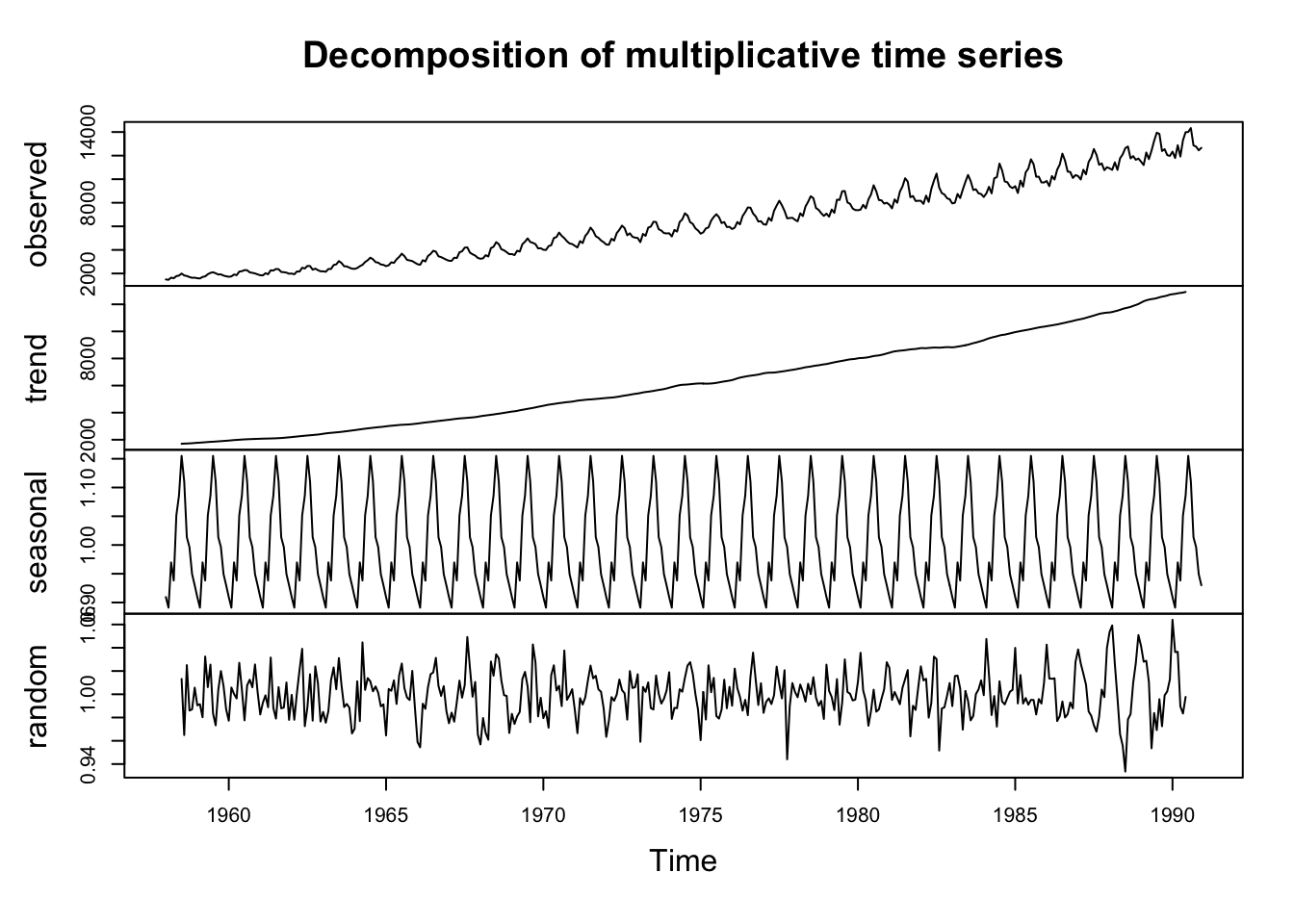

يمكننا ايضا عزل كل عنصر و تمثيلهم في تسلسل زمني واحد عبر الكود التالي

Trend <- Elec.decom$trend
Seasonal <- Elec.decom$seasonal
ts.plot(cbind(Trend, Trend*Seasonal), lty=  1: 2)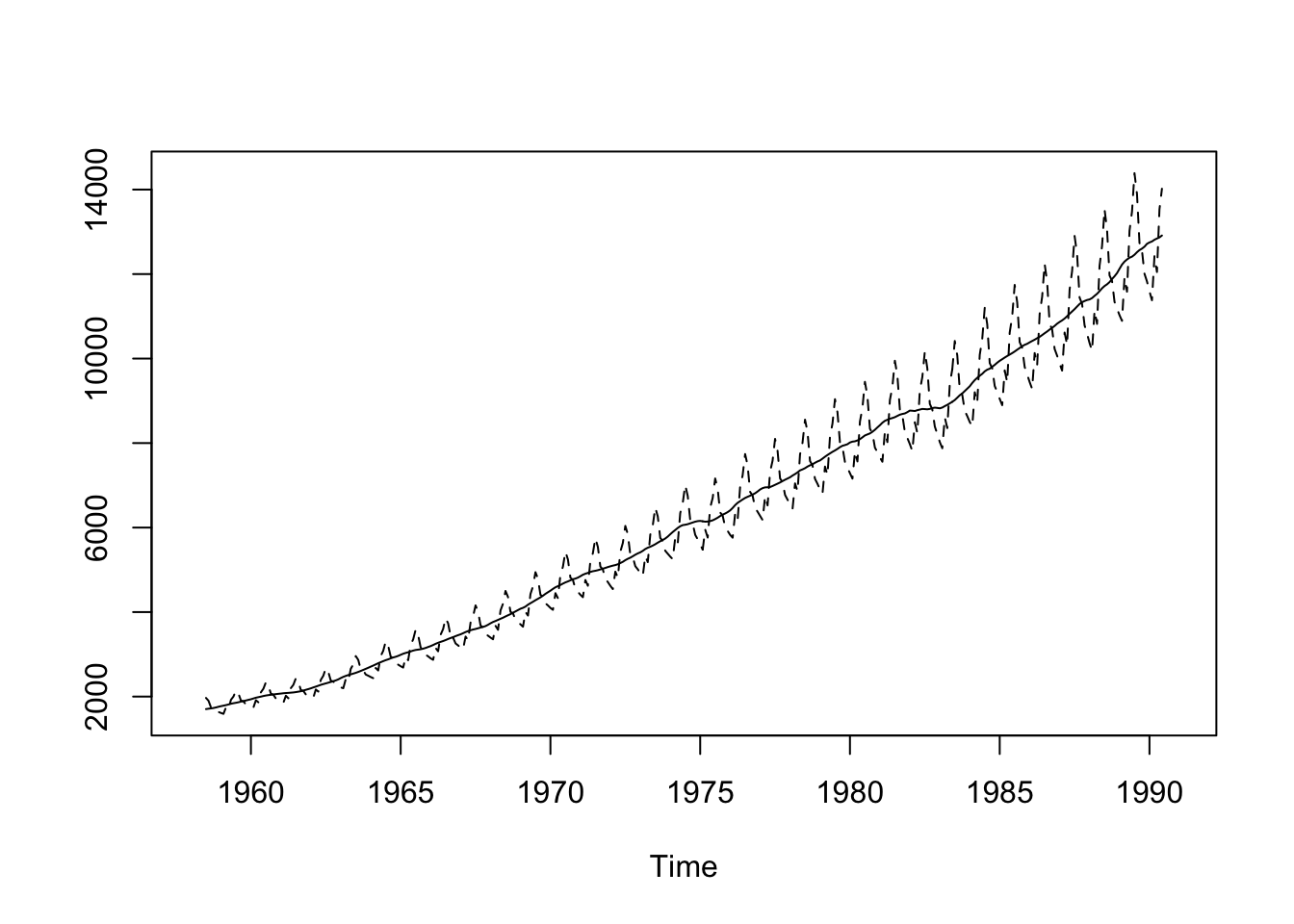

الخلاصة

في هذا المقال تعرفنا اولا على بعض الرموز الرياضية الشائعة في تحليل التسلسلات الزمنية و المهمة لقراءة اي بحث علمي في هذا المجال. ثانيا, قمنا بمعاينة النموذج المبسط للتسلسلات الزمنية ومناقشة عناصره وكيفية تقديرها. أخيرا, ختمنا المقال بمثال عملي تعلمنا من خلال كيفية تفكيك التسلسل الزمني لعناصره الأساسية. اتمنى أن يكون المقال حاز على رضاكم ولكن ايضا اتمنى انكم تعلمتم شي جديد يفيدكم في حياتكم العملية.