نظرة موجزة إلى القيم الشاذة

مقدمة

تخيل أنك مسافر إلى ضواحي فالينسيا في اسبانيا وكونك مهتم بجمع وتحليل البيانات قررت أن ترصد العادات والتقاليد لأفراد الأسرة الاسبانية اليومية. خلال تجولك، لاحظت أن بعض الافراد تمشي بشورتات سباحة ولابسة نظارات واقية. هذا الموضوع اثار انتباهك لأن البحر يبعد أربعين كيلو متر عن القرية الي انت فيها. ما هي إلا دقائق والدنيا تمطر طماطم والناس تتراشق بالطماطم. انت مش عارف أيش الي جالس يصير بس متأكد ان هناك امر غير اعتيادي (امر شاذ) عن المألوف. بعد التحقق وجدت ان اليوم هو آخر يوم اربعاء من شهر أغسطس وهو يوم يحتفل فيه أهالي قرية بونول Bunōl برمي الطماطم على بعضهم البعض (La Tomatina Festival) كذكرى للمظاهرة ضد فرانكو عام ١٩٤٥م.

الإنسان فضولي بطبيعته وهو دائما يحاول إدراك العالم من حوله. هذا الفضول هو من أنجب لنا علم الإحصاء الذي من خلاله تمكنا من تطوير النظريات والمسلمات العلمية. لكن أحيانا كثيرة نصادف قيم استثنائية أو شاذة في إحصاءاتنا لا تمثل النمط أو الاتجاه العام للظاهرة المراد دراستها. القيمة الشاذة في المثال الذي طرحته في المقدمة كان واضحا وسهل الكشف عنه، بل وكان سهل تفسير سبب شذوذ القيمة فيه. لكن ماذا لو كانت القيمة او القيم الشاذة اقل وضوحا؟ أو حتى غير قابلة للتفسير؟

الإجابة على هذا السـؤال وغيره من الأسئلة ليس سهلاً. الأمر الذي دفع ببرنيت و لويس إلى كتابة كتاب كامل في هذا الموضوع ” Outliers in Statistical Data“. لذلك، انصحك ان تحتسي لك كوب من القهوة وتجد لك كرسي مريح لأننا سوف نغوص قليل في المصطلحات والنظريات الإحصائية حول التعامل مع القيم الشاذة.

من المصادفة، أن بحثنا في هذا المقال استثنائي أيضا، فنحن سوف نتفادى طرح التعريف الرسمي للقيمة الشاذة في المقال. السبب هو أن التعريف نفسه يختلف باختلاف طبيعة البيانات والفرضيات المسبقة حولها. ولكن هذا الشيء لن يمنعنا من النظر إلى المصادر المحتملة لشذوذ القيم والطرق المعتمدة للتعامل معها.

المصادر المحتملة لشذوذ القيم

وجود قيم شاذة في مجموعة البيانات dataset له احتمالات كثيرة تتلخص في ثلاث مصادر رئيسية. 1 - المصدر الأول هو التقلب المتأصل inherent variability. أحيانا كثيرة  يكون التقلب متأصل في الجمهرة population . مثلا، التقلب في اطوال الذكور في المملكة يتقلب من شخص إلى آخر. في هذه الحالة طبيعة الشذوذ في أي عينة نحصل عليها عشوائي ولا يوجد طريقة تحديدية deterministic approach لتفسير القيم الشاذة. لذلك، يتوجب علينا إما ان نحتوي تلك القيم عن طريق اتباع طرق إحصائية مرنة ومتينة robust statistics  أو إجراء اختبارات إحصائية للقيم المخالفة discordancy test.  نتائج هذه الاختبارات سوف ترشدنا إلى اما إعادة النظر للتوزيع الأولي المفترض revisit initial model  أو رفع القيم الشاذة إلى دراسة مستقلة identifying outliers for further study أو رفض القيم الشاذة و إخراجها من العينة مع الحفاظ على التوزيع الأولي المفترض.

2 - المصدر الثاني هو الخطـأ في القياس Measurement Error. أحيانا، يكون سبب شذوذ القيمة غير مقصود كعدم كفاءة الأداة المستخدمة في القياس أو نتيجة إلى التقريب الخاطئ للأرقام أو حتى الخطـأ في تسجيل البيانات. إن كانت طبيعة الشذوذ تحديدية ففي هذه الحالة بإمكاننا تصحيح الخطأ عن طريق إعادة أخذ العينة أو تغيير الأداة المستخدمة للقياس. أما اذا كانت طبيعته عشوائية فبإمكاننا علاجها بالطرق المذكورة في المصدر الأول.

3 - المصدر الأخير هو الخطأ في الطريقة نفسها Execution Error. أحيانا تكون طريقتنا في جمع البيانات خاطئة. وأحيانا تكون العينة متحيزة biased sample. في هذه الحالة لا يوجد طبيعة عشوائية للشذوذ. لذلك علاج القيم إما أن يكون عن طريق رفض تلك القيم او تصحيحها أو إعادة أخذ العينة. الصورة ادناه تلخص ما سبق نقاشه

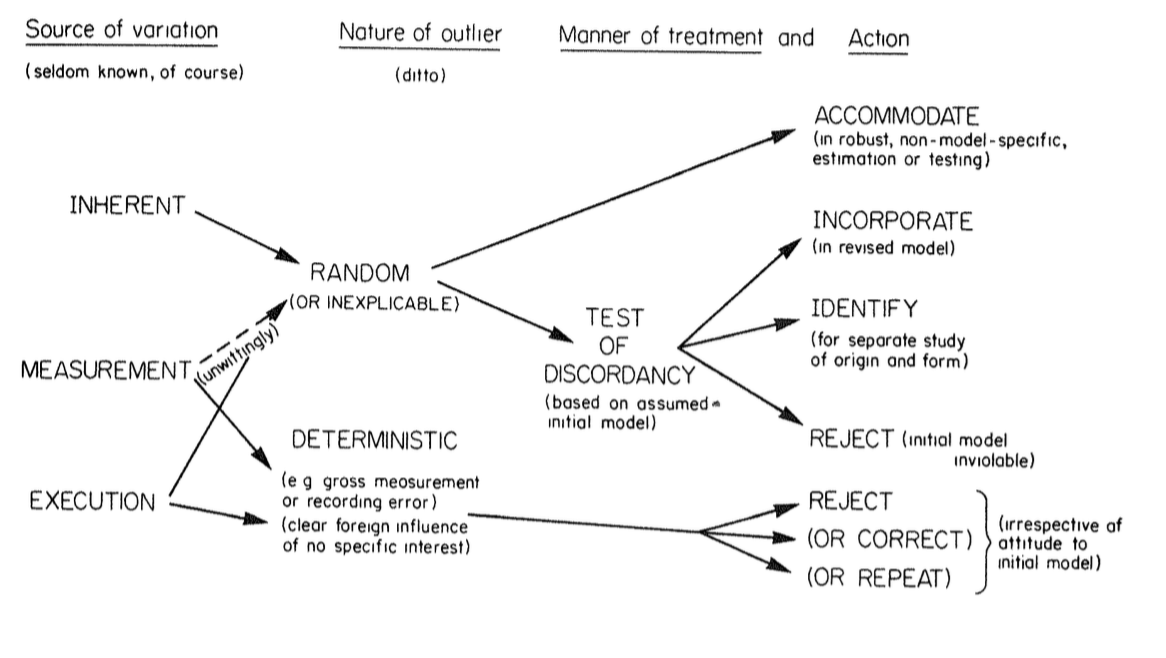
اختبار القيم المخالفة Discordancy Test

لكل اختبار احصائي لابد من وجود فرضية العمل working hypothesis  و الفرضية البديلة alternative hypothesis. اغلب فرضيات العمل تقتضي ان القيمة المراد اختبارها غير شاذة وهي جزء شرعي من التوزيع الأولي المفترض. اما بالنسبة إلى الفرضية البديلة فلقد تعددت الآراء حولها. سوف اذكر تلك الفرضيات مع وصف مختصر.

1 - الفرضية البديلة الأولى هي  Deterministic alternative وهو ان سبب نشوء القيمة الشاذة يمكن تحديده نتيجة لخطأ معين. في هذه الحالة لا يتوجب علينا اجراء أي اختبار. كل ما علينا فعله هو رفض تلك القيم او تصحيح الخطأ.

2 - الفرضية البديلة الثاني هي Inherent alternative  وهو ان سبب نشوء القيمة الشاذة هو عدم كفاءة التوزيع الإحصائي الذي افترضناه للعينة. مثلا، أحيانا كثيرة نفترض ان العينة مأخوذة من جمهرة لها توزيع طبيعي Normal Distribution لكن هذا الافتراض قد لا يكون صحيح. احد الاختبارات المعتمدة والشائعة هي اختبار شابيرو- ويلكShapiro–Wilk test للكشف عن فيما إذا كانت العينة لها توزيع طبيعي ام لا.

3 - الفرضية البديلة الثالثة هي Mixture alternative وهو ان سبب نشوء القيمة الشاذة يعود إلى خطأ في الطريقة المتبعة لجمع البيانات. مثلا، لنفترض اننا نقوم بدراسة احافير نوع معين من الديناصورات، كون أننا لا نعلم بجميع أنواع الديناصورات التي كانت موجودة قمنا عن طريق الخطأ بأخذ احفورة لديناصور مختلف ضمن العينة. للأسف الاختبارات المستخدمة للكشف عن هذا الخطـأ في هذه الحالة لا زالت موضع نقاش بين علماء الإحصاء. ولكن فريق من العلماء قد اعتمد نظرية الاحتمالات القائمة على النظرية البايزية Bayesian Probability. الجدير بالذكر هو ان استخدام هذه الطريقة لا يمكن إلا بفرض قيود كثيرة وبعضها غير عملية.

4 - الفرضية البديلة الرابعة هي Slippage alternative وتنص هذه الفرضية على ان البيانات الموجودة في العينة تنتمي إلى التوزيع الأولي المفترض ما عدا عدد قليل منها ينتمي إلى نفس التوزيع لكن بمعيار إنحرافي او متوسط حسابي مختلف. مثلا، خلينا نقول ان العينة التي نمتلكها لها توزيع طبيعي بمتوسط حسابي ومعيار انحرافي معروفين لكن عدد من البيانات منها ينتمي إلى نفس التوزيع ونفس المتوسط الحسابي لكن بمعيار انحرافي مختلف. هذه الفرضية هي الأكثر شيوعا والأكثر بحثاً وسط علماء الإحصاء. نتيجة لذلك، هناك عدد كبير من الاختبارات المخصصة لكل نوع من التوزيعات الإحصائية التي يمكننك التفكير بها.

هذه اهم الفرضيات البديلة التي يستخدمها علماء الإحصاء للكشف والتعامل مع القيم الشاذة. في المقال القادم سوف نركز بإذن الله اهتمامنا على الاختبارات الإحصائية المستخدمة لتعيين القيم المخالفة Discordancy Tests في حالة اتخاذ الفرضية البديلة الأخيرة. وبل وسوف نناقش بشكل خاص تلك الاختبارات في حالة تبني توزيع الغاماGamma Distribution  او التوزيع الأسي Exponential Distribution.

ختام

إلى ذلك الوقت أتمنى أنك استمتعت بقراءة هذا المقال. ولكن الأهم من ذلك أتمنى أنك تعلمت شيء جديد عن القيم الشاذة وطريقة التعامل معها.